A Set as a Collection of Elements
A Set as a Collection of Elements
Fundamentals of a Set
Introduction
A set is a list of items with various goals:
To support sets, the .NET Framework provides a class named HashSet. This class is created in the System.Collections.Generic namespace.
In algebra, a set is usually represented with an uppercase letter, such as A. In programming, we will represent the list with a name.
Consider the following list and notice that it contains an item twice:
namespace Dictionaries
{
public partial class Exercise : Form
{
public Exercise()
{
InitializeComponent();
}
private void InitializeComponent()
{
}
private void Exercise_Load((object sender, EventArgs ea)
{
List<string> names = new List<string>();
names.Add("Kevin");
names.Add("Jane");
names.Add("Daniel");
names.Add("Ruth");
names.Add("Jane");
names.Add("Paul");
lbxNames.DataSource = names;
}
}
}
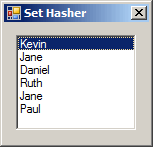
In a .NET application, a set is a list that does not allow duplicate items.
Most of the time, in algebra, to study sets, we use numbers. In all of the examples in this lesson, we will use strings to make them more interesting. Obviously, integers would be easier. If you want to use numbers, all you have to do is to replace all strings in our examples with numbers. |
![]() Practical Learning: Introducing Sets
Practical Learning: Introducing Sets
| Control | Text | Name | |
| Label | Number: | ||
| TextBox | txtNumberA | ||
| Button | Add | btnAddA | |
| ListBox | Numbers | ||
Creating an Empty Set
In algebra, a set is empty if it contains no element. This is the case for a brand new set. It can also happen if the elements in the set have been deleted. In algebra, to create an empty set, use an uppercase letter and assign the phi character to it. Here is an example:
A = ∅
(In algebra, an empty set is also called a null set.) In algebra, to visually represent a set, we draw a circle. If the set is empty, the circle is blank:

To programmatically create an empty set, declare a variable of type HashSet<> and use the new operator to initialize it.
Depending on the type of series, one set can be made of natural numbers, another made of floating-point numbers, yet another one made of strings or other types of values (dates, times, etc). When programmatically creating a set, pass the type of items in the angle brackets. Here is an example:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> names = new HashSet<string>();
}
The HashSet<> class starts as follows:
public class HashSet<T> : System.Collections.Generic.ICollection<T>,
System.Collections.Generic.IEnumerable<T>,
System.Collections.Generic.IReadOnlyCollection<T>,
System.Collections.Generic.IReadOnlySet<T>,
System.Collections.Generic.ISet<T>,
System.Runtime.Serialization.IDeserializationCallback,
System.Runtime.Serialization.ISerializable
![]() Practical Learning: Creating an Empty Set
Practical Learning: Creating an Empty Set
namespace SetsAndSeries
{
public partial class Algebra : Form
{
HashSet<int>? A;
public Algebra()
{
InitializeComponent();
}
private void Algebra_Load(object sender, EventArgs e)
{
A = new HashSet<int>();
}
}
}Fundamental Operations on a Set
Populating a Set
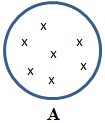
Unless a set is empty, it must have or contain something. An object included in a set is called an element or a member of the set. In algebra, to create a set, we specify an uppercase letter, followed by = { }. In the curly brackets, we list the elements separated by commas. Here is an example:
A = { Kevin, Jane, Daniel, Ruth, Paul }
To visually illustrate, you can represent each element in the circle. Here is an example:
To let create a set, the HashSet<> class is equipped with a method named Add. Its syntax is:
public bool Add(T item);
Call this method to add a new item to the set. Here are examples:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> names = new HashSet<string>();
names.Add("Kevin");
names.Add("Jane");
names.Add("Daniel");
names.Add("Ruth");
names.Add("Paul");
foreach (string str in names)
lbxNames.Items.Add(str);
}
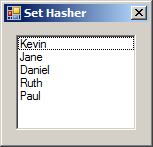
Notice that each element in this case is a constant, or has a constant value.
Remember that one of the rules of a set is that it cannot have duplicate items. If you add an item that exists in the list already, that item would not be added. In fact, to let you know whether an item was added, the HashSet<>.Add() method returns a Boolean value:
The following code will illustrate:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> names = new HashSet<string>();
if (names.Add("Kevin") == true)
MessageBox.Show("Kevin has been added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("Kevin was not added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (names.Add("Jane") == true)
MessageBox.Show("Jane has been added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("Jane was not added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (names.Add("Daniel") == true)
MessageBox.Show("Daniel has been added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("Daniel was not added to the list");
if (names.Add("Ruth") == true)
MessageBox.Show("Ruth has been added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("Ruth was not added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (names.Add("Jane") == true)
MessageBox.Show("Jane has been added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("Jane was not added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (names.Add("Paul") == true)
MessageBox.Show("Paul has been added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("Paul was not added to the list.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
foreach (string str in names)
lbxNames.Items.Add(str);
}
 |
 |
 |
 |
 |
 |
![]() Practical Learning: Populating a Set
Practical Learning: Populating a Set
namespace SetsAndSeries
{
public partial class Algebra : Form
{
HashSet<int>? A;
public Algebra()
{
InitializeComponent();
}
private void Algebra_Load(object sender, EventArgs e)
{
A = new HashSet<int>();
}
private void btnAddA_Click(object sender, EventArgs e)
{
int x = 0;
try
{
x = int.Parse(txtNumberA.Text);
A!.Add(x);
}
catch (FormatException)
{
MessageBox.Show("The value you typed is not a valid number.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
lbxNumbersA.Items.Clear();
foreach (int element in A)
lbxNumbersA.Items.Add(element);
txtNumberA.Text = "";
txtNumberA.Focus();
}
}
}
The Number of Items in a Set
In algebra, when it comes to the number of elements in a set, there are two categories. A set is referred to as finite it contains a constant number of items. An example is the number of students in a classroom. A set is infinite if its number of items cannot be counted. An example is the number of stars in the sky.
The HashSet<> class implements the ICollection<> generic interface, which gives it a property named Count. This property allows you to know the number of elements in a set. Here is an example:
namespace SetsAndSeries
{
public partial class Exercise : Form
{
public Exercise()
{
InitializeComponent();
}
private void Exercise_Load(object sender, EventArgs e)
{
HashSet<string> names = new HashSet<string>();
names.Add("Kevin Walchild");
names.Add("Jane Overton");
names.Add("Daniel Albertson");
names.Add("Ruth Oyawale");
names.Add("Jane Ouelette");
names.Add("Paul Sullivan");
foreach (string str in names)
lbxNames.Items.Add(str);
lblCount.Text = "The list contains " + names.Count.ToString() + " items";
}
}
}
Checking Whether a Set Contains a Certain Element
In algebra, to represent that a certain value "a" exists in a set A, we may write:
a ∈ A
This is read as "a is an element of set A" or "a is included in set A" or "Set A contains a". To support this operation, the HashSet<> class inherits the Contains() method from the ICollection<> interface. The method allows you to check whether the list already contains a certain item. Here are examples of calling this method:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> names = new HashSet<string>();
names.Add("Kevin Walchild");
names.Add("Jane Overton");
names.Add("Daniel Albertson");
names.Add("Ruth Oyawale");
names.Add("Jane Ouelette");
names.Add("Paul Sullivan");
foreach (string str in names)
lbxNames.Items.Add(str);
if( names.Contains("Jane Owerton") )
MessageBox.Show("The list contains Jane Owerton.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The list doesn't contain Jane Owerton",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( names.Contains("Jane Overton") )
MessageBox.Show("The list contains Jane Overton.",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The list doesn't contain Jane Overton",
"Hash Set Operations",
MessageBoxButtons.OK, MessageBoxIcon.Information);
lblCount.Text = "The list contains " + names.Count.ToString() + " items";
}
 |
 |
In algebra, to state that an element a is not in the set A, we write:
a ∉ A
This reads "a is not an element of set A" or "a is not included in set A" or "Set A does not contain a". To perform this checking in programming, you can use the NOT operator "!".
Creating a Duplicate Set
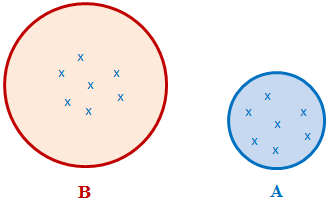
In algebra, after creating a set A, you may want to create another set B but that contains the same elements as A. To do this, you can simply assign the elements of A to B. This would be done as follows:
A = { Kevin Walchild, Jane Overton, Daniel Albertson,
Ruth Oyawale, Jane Ouelette, Paul Sullivan }
B = A
Now, sets A and B have the same elements:
To support this operation, the HashSet<> class provides another constructor (in some languages like C++ and Pascal, this type of constructor is called a copy constructor) whose syntax is:
public HashSet(IEnumerable<T> collection);
This constructor allows you to create a new set that is made of values from an existing set. You create the new list by passing the name of the existing list to this constructor. Here is an example:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> names = new HashSet<string>();
names.Add("Kevin Walchild");
names.Add("Jane Overton");
names.Add("Daniel Albertson");
names.Add("Ruth Oyawale");
names.Add("Jane Ouelette");
names.Add("Paul Sullivan");
HashSet<string> people = new HashSet<string>(names);
}
Once you have created the list, you can manipulate it as you see fit. For example, you can add new items to it. Here is an example:
namespace SetsAndSeries
{
public partial class Exercise : Form
{
public Exercise()
{
InitializeComponent();
}
private void Exercise_Load(object sender, EventArgs e)
{
HashSet<string> names = new();
names.Add("Kevin Walchild");
names.Add("Jane Overton");
names.Add("Daniel Albertson");
names.Add("Ruth Oyawale");
names.Add("Jane Ouelette");
names.Add("Paul Sullivan");
foreach (string str in names)
lbxNames.Items.Add(str);
lblCount.Text = "Number of items: " + names.Count.ToString();
HashSet<string> people = new HashSet<string>(names);
people.Add("Antoinette Belton");
people.Add("Joshua Melmann");
foreach (string str in people)
lbxPeople.Items.Add(str);
lblPeople.Text = "Number of items: " + people.Count.ToString();
}
}
}
![]() Practical Learning: Duplicating a Set
Practical Learning: Duplicating a Set
| Control | Text | Name | |
| Label | Number: | ||
| TextBox | txtNumberA | ||
| Button | Add | btnAddNumberA | |
| ListBox | lbxNumbersA | ||
| Button | Duplicate | btnDuplicate | |
| ListBox | lbxNumbersB | ||
namespace SetsAndSeries
{
public partial class Algebra : Form
{
HashSet<int>? A;
HashSet<int>? B;
public Algebra()
{
InitializeComponent();
}
private void Algebra_Load(object sender, EventArgs e)
{
A = new HashSet<int>();
B = new HashSet<int>();
}
private void btnAddA_Click(object sender, EventArgs e)
{
int x;
try
{
x = int.Parse(txtNumberA.Text);
A!.Add(x);
}
catch (FormatException)
{
MessageBox.Show("The value you typed is not a valid number.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
lbxNumbersA.Items.Clear();
foreach (int element in A)
lbxNumbersA.Items.Add(element);
txtNumberA.Text = "";
txtNumberA.Focus();
}
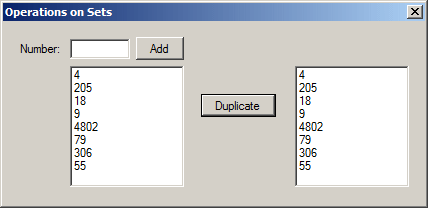
private void btnDuplicate_Click(object sender, EventArgs e)
{
B = A;
foreach (int element in B)
lbxNumbersB.Items.Add(element);
}
}
}
Operations on Sets
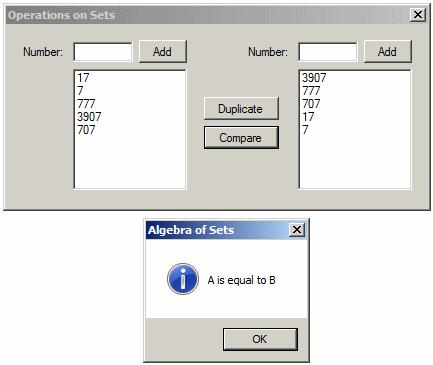
Comparing For Equality
Imagine you have two sets A and B defined as follows:
A = { Kevin Walchild, Jane Overton, Daniel Albertson, Jane Ouelette }
B = { Daniel Albertson, Kevin Walchild, Jane Ouelette, Jane Overton }
Notice that both sets have the same elements. When two sets have exact same members, we say that those sets are equal. This can be expressed as:
A = B
This operation is commutative, which means the above operation can also be written as:
B = A
We already know that all classes used in a C# application (or a .NET project) derive from the Object class and they inherit a method named Equals. This makes it possible to compare two values or two objects for equality. The HashSet<> class also naturally inherits this method. Although you can use that method, the HashSet<> class provides its own custom method named SetEquals. Its syntax is:
public bool SetEquals(IEnumerable<T> other);
This method takes as argument another HashSet<> list and compares both sets. If the sets are the same, the method returns true. Otherwise it produces a false value. Here are examples of calling this method:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> names = new HashSet<string>();
names.Add("Kevin Walchild");
names.Add("Jane Overton");
names.Add("Daniel Albertson");
names.Add("Ruth Oyawale");
names.Add("Jane Ouelette");
names.Add("Paul Sullivan");
foreach (string str in names)
lbxNames.Items.Add(str);
lblCount.Text = "Number of items: " + names.Count.ToString();
HashSet<string> people = new HashSet<string>(names);
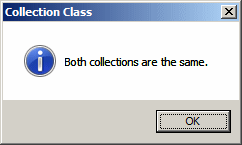
if (people.SetEquals(names) == true)
MessageBox.Show("Both collections are the same.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("These collections are different.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
people.Add("Antoinette Belton");
people.Add("Joshua Melmann");
if (people.SetEquals(names) == true)
MessageBox.Show("Both collections are the same.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("These collections are different.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
foreach (string str in people)
lbxPeople.Items.Add(str);
lblPeople.Text = "Number of items: " + people.Count.ToString();
}
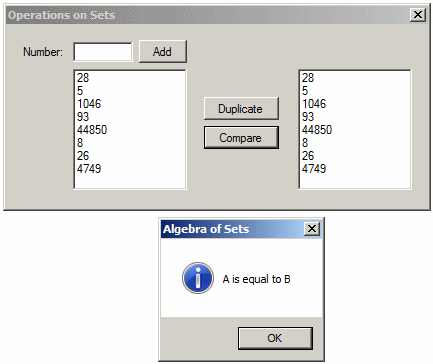
![]() Practical Learning: Comparing For Equality
Practical Learning: Comparing For Equality
| Control | Text | Name | |
| Button | Compare | btnCompare | |
private void btnCompare_Click(object sender, EventArgs e)
{
if (A.SetEquals(B))
MessageBox.Show("A is equal to B",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
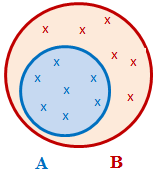
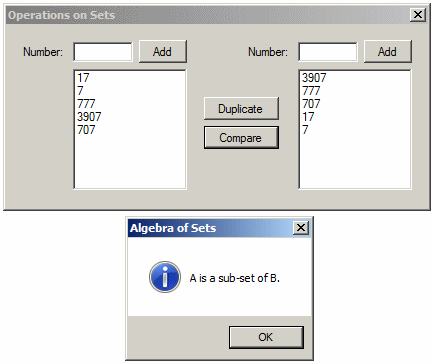
A Subset of Another Set
Imagine you have two sets A and B defined as follows:
A = { Kevin, Jane, Daniel }
B = { Raul, Kevin, Tiffany, Daniel, Michael, Jane, Paul }
Notice that all members of A are also members of B. In algebra, to express this, we write:
A ⊂ B
This is the same as:
{ Kevin, Jane, Daniel } ⊂ { Raul, Kevin, Tiffany, Daniel, Michael, Jane, Paul }
We say that A is a subset of B. This can be visually illustrated as follows:
In algebra, any set is a subset of itself. Also, since the empty set doesn't have any element, the empty set is a subset of any set. We write it as:
∅ ⊂ A
and
∅ ⊂ B
An empty set is also a subset of itself.
To let you find out you whether one set is a subset of another, the HashSet<> class is equipped with a method named IsSubsetOf(). Its syntax is:
public bool IsSubsetOf(IEnumerable<T> other);
If the set passed as argument is a subset of the variable that called the method, the method returns true. Otherwise, it returns false. Here is an example of calling this method:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> Persons = new HashSet<string>();
Persons.Add("Kevin Walchild");
Persons.Add("Jane Overton");
Persons.Add("Daniel Albertson");
HashSet<string> People = new HashSet<string>();
People.Add("Raul Fitzgerald");
People.Add("Kevin Walchild");
People.Add("Tiffany Morales");
People.Add("Daniel Albertson");
People.Add("Michael Rhodia");
People.Add("Ruth Oyawale");
People.Add("Jane Overton");
People.Add("Paul Sullivan");
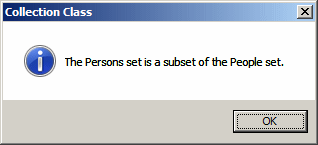
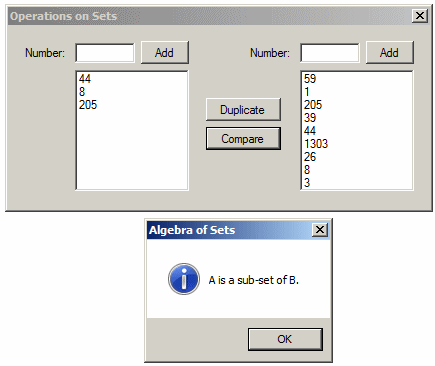
if (Persons.IsSubsetOf(People))
MessageBox.Show("The Persons set is a subset of the People set.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The Persons set is not a subset of the People set.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
foreach (string str in Persons)
lbxNames.Items.Add(str);
lblCount.Text = "Number of items: " + Persons.Count.ToString();
foreach (string str in People)
lbxPeople.Items.Add(str);
lblPeople.Text = "Number of items: " + People.Count.ToString();
}
It is important to know that the subset relationship is one way; in other words, the comparison is not commutative: the fact that a set A is a subset of a set B is not vice-versa.
![]() Practical Learning: Checking for Sub-Set
Practical Learning: Checking for Sub-Set
| Control | Text | Name | |
| Label | Number: | ||
| TextBox | txtNumberA | ||
| Button | Add | btnAddNumberA | |
| Label | Number: | ||
| TextBox | txtNumberB | ||
| Button | Add | btnAddNumberB | |
namespace SetsAndSeries
{
public partial class Algebra : Form
{
HashSet<int>? A;
HashSet<int>? B;
public Algebra()
{
InitializeComponent();
}
private void Algebra_Load(object sender, EventArgs e)
{
A = new HashSet<int>();
B = new HashSet<int>();
}
private void btnAddA_Click(object sender, EventArgs e)
{
int x;
try
{
x = int.Parse(txtNumberA.Text);
A!.Add(x);
}
catch (FormatException)
{
MessageBox.Show("The value you typed is not a valid number.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
lbxNumbersA.Items.Clear();
foreach (int element in A)
lbxNumbersA.Items.Add(element);
txtNumberA.Text = "";
txtNumberA.Focus();
}
private void btnDuplicate_Click(object sender, EventArgs e)
{
B = A;
foreach (int element in B)
lbxNumbersB.Items.Add(element);
}
private void btnCompare_Click(object sender, EventArgs e)
{
if (A.SetEquals(B))
MessageBox.Show("A is equal to B",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSubsetOf(B))
MessageBox.Show("A is a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
private void btnAddB_Click(object sender, EventArgs e)
{
int x = 0;
try
{
x = int.Parse(txtNumberB.Text);
B.Add(x);
}
catch (FormatException)
{
MessageBox.Show("The value you typed is not a valid number.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
lbxNumbersB.Items.Clear();
foreach (int element in B)
lbxNumbersB.Items.Add(element);
txtNumberB.Text = "";
txtNumberB.Focus();
}
}
}
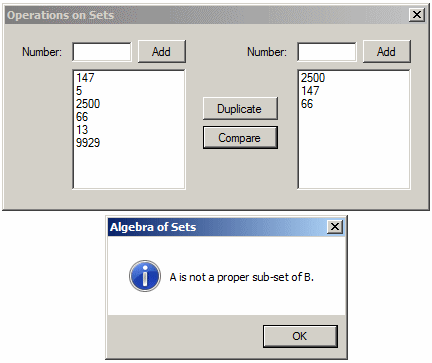
A Proper Subset of Another Set
A set is a subset of itself. Also, when two sets have the exact same members, each set is a subset of the other:
On the other hand, if you have a set A that is strictly a subset of another set B, this means there is at least one element in set B that is not a member of set A. In this case, we say that set A is a proper subset of set B. This can be illustrated as follows:

To let you find out if a set is a proper subset of another set, the HashSet<> class is equipped with a method named IsProperSubsetOf. Its syntax is:
public bool IsProperSubsetOf(IEnumerable<T> other);
This method takes a HashSet<> value as arguments and performs a comparison on the elements of both sets (the set that called this method and the set that was passed as argument):
Here are two examples of calling this method:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> Persons = new HashSet<string>();
Persons.Add("Kevin Walchild");
Persons.Add("Frank Maguire");
Persons.Add("Jane Overton");
Persons.Add("Daniel Albertson");
HashSet<string> Students = new HashSet<string>();
Students.Add("Jane Overton");
Students.Add("Kevin Walchild");
Students.Add("Daniel Albertson");
Students.Add("Frank Maguire");
HashSet<string> People = new HashSet<string>();
People.Add("Raul Fitzgerald");
People.Add("Kevin Walchild");
People.Add("Tiffany Morales");
People.Add("Daniel Albertson");
People.Add("Michael Rhodia");
People.Add("Frank Maguire");
People.Add("Ruth Oyawale");
People.Add("Jane Overton");
People.Add("Paul Sullivan");
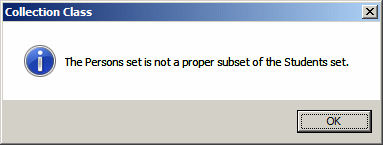
if (Persons.IsProperSubsetOf(Students))
MessageBox.Show("The Persons set is a proper subset of the Students set.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The Persons set is not a proper subset of the Students set.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
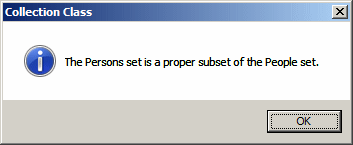
if (Persons.IsProperSubsetOf(People))
MessageBox.Show("The Persons set is a proper subset of the People set.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The Persons set is not a proper subset of the People set.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
![]() Practical Learning: Checking for Proper Sub-Set
Practical Learning: Checking for Proper Sub-Set
private void btnCompare_Click(object sender, EventArgs e)
{
if (A.SetEquals(B))
MessageBox.Show("A is equal to B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsSubsetOf(B))
MessageBox.Show("A is a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsProperSubsetOf(B))
MessageBox.Show("A is a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
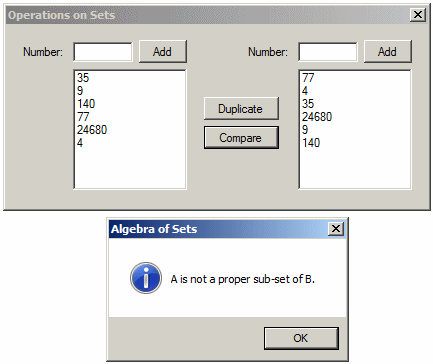
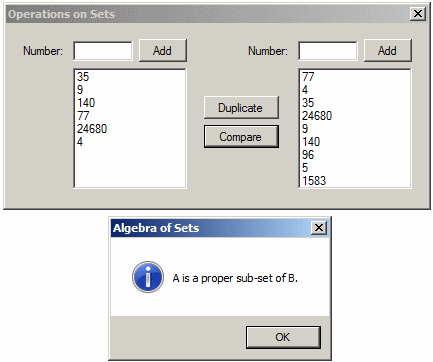
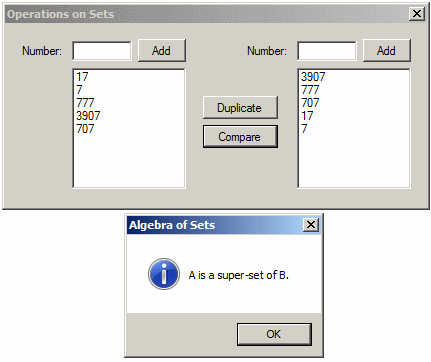
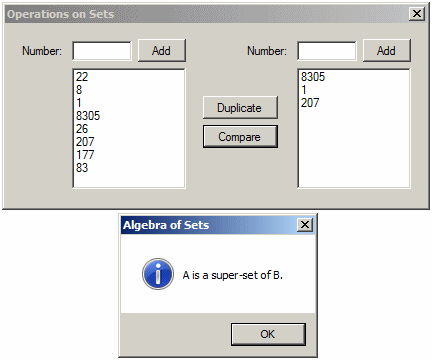
A Super-Set of an Existing Set
Remember that a sub-set is a set whose all elements are also found in another set. A super-set is the reverse of a sub-set. That is, in a superset, all the elements of a set B are found in a set A but set A may have elements that are not found in B. In algebra, this can be written as follows:
B ⊃ A
To help you make this comparison, the HashSet<> class is equipped with a method named IsSupersetOf. Its syntax is:
public bool IsSupersetOf(IEnumerable<T> other);
This method takes a HashSet<> object as argument and compares its elements to those of the variable that called it. If all the elements of the argument are found in the variable that called it, the method returns true.
![]() Practical Learning: Checking for Super-Set
Practical Learning: Checking for Super-Set
private void btnCompare_Click(object sender, EventArgs e)
{
if (A.SetEquals(B))
MessageBox.Show("A is equal to B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSubsetOf(B))
MessageBox.Show("A is a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSupersetOf(B))
MessageBox.Show("A is a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsProperSubsetOf(B))
MessageBox.Show("A is a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}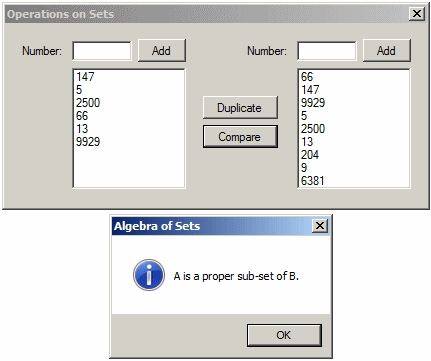
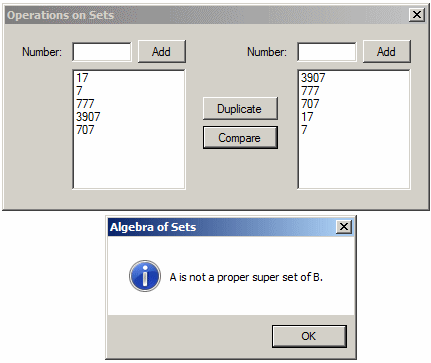
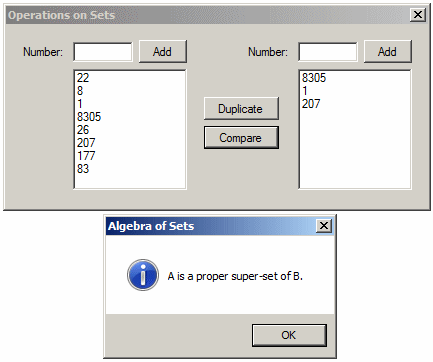
A Proper Super-Set of an Existing Set
When it comes to a super-set, if both sets are the same, each is considered a super-set of the other and the IsSupersetOf() method returns true. By contrast, if a set B is a super-set of A but both sets are not the same, that is, set B has more elements than set A, set B is said to be a property super-set of A. To let you make the comparison to determine this, the HashSet<> class provides a method named IsProperSupersetOf. Its syntax is:
public bool IsProperSupersetOf(IEnumerable<T> other);
![]() Practical Learning: Checking for a Proper Super-Set
Practical Learning: Checking for a Proper Super-Set
private void btnCompare_Click(object sender, EventArgs e)
{
if (A.SetEquals(B))
MessageBox.Show("A is equal to B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsSubsetOf(B))
MessageBox.Show("A is a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSupersetOf(B))
MessageBox.Show("A is a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsProperSubsetOf(B))
MessageBox.Show("A is a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsProperSupersetOf(B))
MessageBox.Show("A is a proper super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper super set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
A Union of Two Sets
Imagine you have two sets A and B defined as follows:
A = { Kevin, Jane, Daniel }
B = { Raul, Kevin, Tiffany, Michael, Jane }
One of the operations you can perform on them is to create a set that contains a list of all their elements. That is, you would get a list that contains elements that are present in each set. If there is an element present in both sets, it would be included only once.
A union of two sets is the list of all elements that belong to both sets. Remember that there is no reason to include an element twice if it already belongs to one of the sets. In algebra, this operation is written as follows:
A ∪ B = { x|x ∈ A or x ∈ B }
This can be visually illustrated as follows:
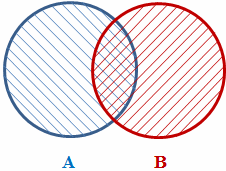
To help you unite two sets, the HashSet<> class is equipped with a method named UnionWith. Its syntax is:
public void UnionWith(IEnumerable<T> other);
This method takes as argument the set whose elements would be combined to those of the set that called the method. Here is an example of calling this method:
namespace SetsAndSeries
{
public partial class Exercise : Form
{
public Exercise()
{
InitializeComponent();
}
private void Exercise_Load(object sender, EventArgs e)
{
HashSet<string> persons = new HashSet<string>();
persons.Add("Kevin Walchild");
persons.Add("Jane Overton");
persons.Add("Daniel Albertson");
persons.Add("Ruth Oyawale");
persons.Add("Jane Ouelette");
foreach (string str in persons)
lbxPersons.Items.Add(str);
lblPersons.Text = "Number of items: " + persons.Count.ToString();
HashSet<string> people = new HashSet<string>();
people.Add("Antoinette Belton");
people.Add("Joshua Melmann");
people.Add("Paul Sullivan");
foreach (string str in people)
lbxPeople.Items.Add(str);
lblPeople.Text = "Number of items: " + people.Count.ToString();
persons.UnionWith(people);
foreach (string str in persons)
lbxPersonsUnionPeople.Items.Add(str);
lblPersonsUnionPeople.Text = "Number of items: " + persons.Count.ToString();
}
}
}
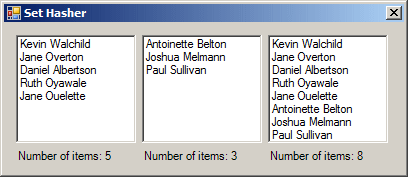
It is important to know that this method performs a comparison on the elements of both sets so that the result would not allow any duplicate item.
![]() Practical Learning: Creating a Union of Two Sets
Practical Learning: Creating a Union of Two Sets
| Control | Text | Name | |
| Button | Union | btnUnion | |
| ListBox | lbxUnion | ||
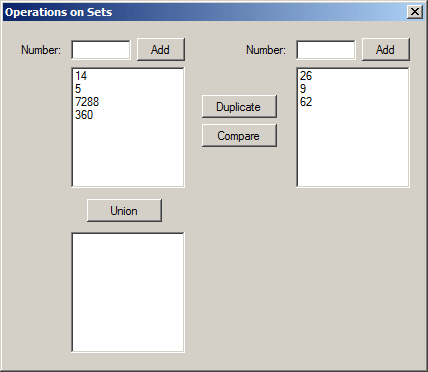
private void btnUnion_Click(object sender, EventArgs e)
{
// Because objects in C# are used as references,
// we will need a brand new set that has the same
// elements as set A
HashSet<int> Union = new HashSet<int>();
// Copy the elements of A into the new set
foreach(int element in A)
Union.Add(element);
// Unite the new set to B
Union.UnionWith(B);
lbxUnion.Items.Clear();
foreach (int element in Union)
lbxUnion.Items.Add(element);
}
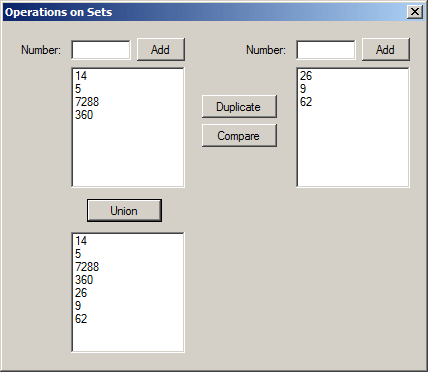
A Universal Set
If you have two or more sets, a universal set is a list that contains all elements of those sets. For example, if you have three sets A, B, and C, you can write their universal set as:
A ∪ B ∪ C
To programmatically create a universal set, simply call the HashSet<>.UnionWith() method as necessary.
An Intersection of Sets
The intersection between two sets is the list of only members that belong to both sets. That is, the elements that belong to one set but do not belong to the other set are excluded. In algebra, we write it as follows:
A ∩ B = { x|x ∈ A and x ∈ B }
This can be visually illustrated as follows:
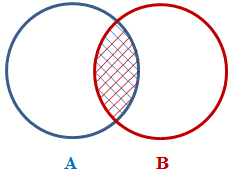
To help you reduce a set to its intersecting elements with regards to another set, the HashSet<> class provides the IntersectWith() method. Its syntax is:
public void IntersectWith(IEnumerable<T> other);
This takes a HashSet<> object as argument. It finds the elements from the argument that are also present in the variable that called it and it removes the elements that are found in the variable that called it but are not found in the argument.
![]() Practical Learning: Creating a Union of Two Sets
Practical Learning: Creating a Union of Two Sets
| Control | Text | Name | |
| Button | Intersection | btnIntersection | |
| ListBox | lbxIntersection | ||
private void btnIntersection_Click(object sender, EventArgs e)
{
HashSet<int> Intersection = new HashSet<int>();
foreach (int element in A)
Intersection.Add(element);
Intersection.IntersectWith(B);
lbxIntersection.Items.Clear();
foreach (int element in Intersection)
lbxIntersection.Items.Add(element);
}
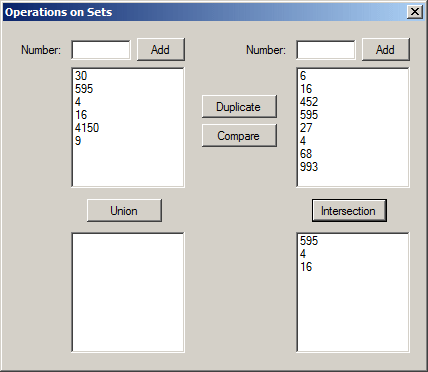
Overlapped Sets
As seen above, the intersecting set is a list of elements shared by two sets. The comparison consists of finding out whether two lists intersect; that is, whether they have at least one common member. To let you perform this comparison, the HashSet<> class is equipped with a method named Overlaps. Its syntax is:
public bool Overlaps(IEnumerable<T> other);
This method too takes a HashSet<> object as argument and compares it to the object that called it. If it finds at least one value that exists in both lists, the method returns true. If there is no single value that both lists share, the method returns false. Here are two examples of calling this method:
private void Exercise_Load((object sender, EventArgs ea)
{
HashSet<string> Persons = new HashSet<string>();
Persons.Add("Kevin Walchild");
Persons.Add("Jane Overton");
Persons.Add("Daniel Albertson");
Persons.Add("Ruth Oyawale");
Persons.Add("Jane Ouelette");
Persons.Add("Paul Sullivan");
foreach (string str in Persons)
lbxNames.Items.Add(str);
lblCount.Text = "Number of items: " + Persons.Count.ToString();
HashSet<string> People = new HashSet<string>();
People.Add("Antoinette Belton");
People.Add("Joshua Melmann");
People.Add("Deborah Callum");
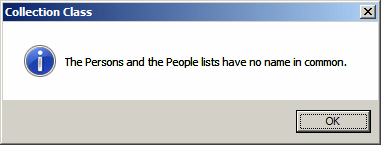
if (People.Overlaps(Persons) == true)
MessageBox.Show("The Persons and the People lists have at least one name in common.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The Persons and the People lists have no name in common.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
foreach (string str in People)
lbxPeople.Items.Add(str);
lblPeople.Text = "Number of items: " + People.Count.ToString();
HashSet<string> Students = new HashSet<string>();
Students.Add("Dominique Donahue");
Students.Add("Daniel Albertson");
Students.Add("Michael Sorenso");
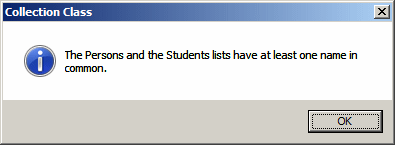
if (Students.Overlaps(Persons))
MessageBox.Show("The Persons and the Students lists have at least one name in common.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("The Persons and the Students lists have no name in common.",
"Collection Class",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
![]() Practical Learning: Checking for a Overlapping Sets
Practical Learning: Checking for a Overlapping Sets
private void btnCompare_Click(object sender, EventArgs e)
{
if (A.SetEquals(B))
MessageBox.Show("A is equal to B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsSubsetOf(B))
MessageBox.Show("A is a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSupersetOf(B))
MessageBox.Show("A is a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if( A.IsProperSubsetOf(B))
MessageBox.Show("A is a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsProperSupersetOf(B))
MessageBox.Show("A is a proper super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper super set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
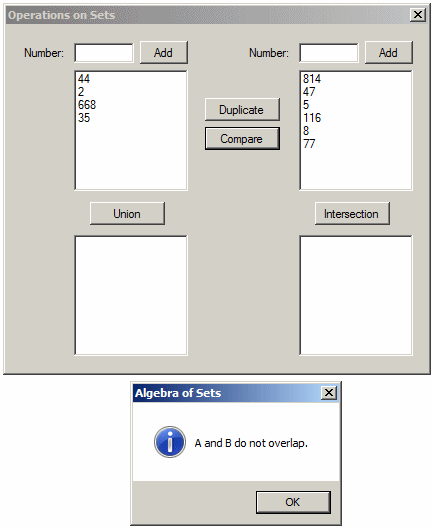
if (A.Overlaps(B))
MessageBox.Show("A and B overlap.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A and B do not overlap.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
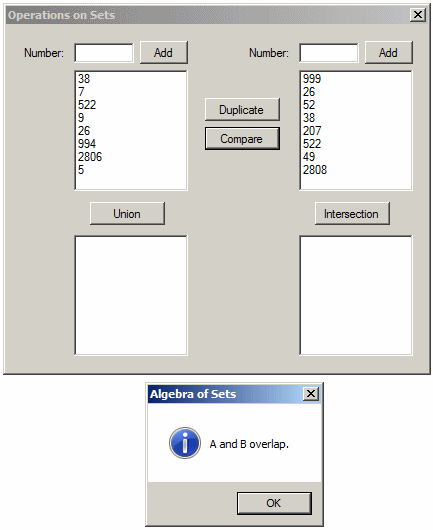
Set Difference
Consider two sets A and B. The difference between a set A from a set B is the list of elements that are found in set A but are not found in set B. In algebra, this is written as follows:
A - B = { x|x ∈ A and x ∉ B }
This can be illustrated as follows:
To let you perform this operation, the HashSet<> class provides a method named ExceptWith. Its syntax is:
public void ExceptWith(IEnumerable<T> other);
![]() Practical Learning: Getting the Difference of Two Sets
Practical Learning: Getting the Difference of Two Sets
| Control | Text | Name | |
| Button | Difference | btnDifference | |
| ListBox | lbxDifference | ||
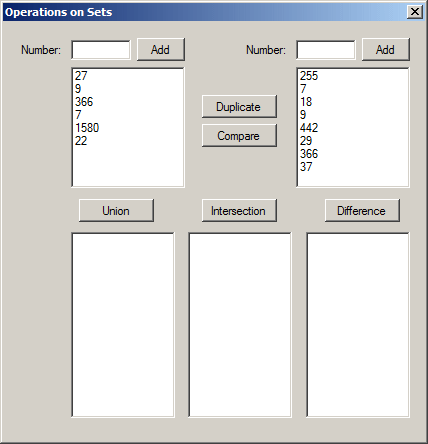
private void btnDifference_Click(object sender, EventArgs e)
{
HashSet<int> Difference = new HashSet<int>();
foreach (int element in A)
Difference.Add(element);
Difference.ExceptWith(B);
lbxDifference.Items.Clear();
foreach (int element in Difference)
lbxDifference.Items.Add(element);
}
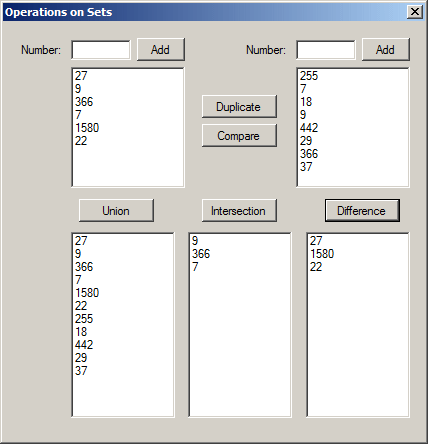
Symmetric Difference
Consider two sets A and B. The symmetric difference between those sets is the list of elements that belong to each set but do not belong to their intersection. This can be illustrated as follows:
As you can guess, this is the reverse of the intersection. That is, it is the union of the sets excluding their intersection. To let you perform this operation, the HashSet<> class is equipped with a method named SymmetricExceptWith. Its syntax is:
public void SymmetricExceptWith(IEnumerable<T> other);
![]() Practical Learning: Getting the Symmetric Difference of Two Sets
Practical Learning: Getting the Symmetric Difference of Two Sets
| Control | Text | Name | |
| Button | Symmetric Difference | btnSymmetricDifference | |
| ListBox | lbxSymmetricDifference | ||
private void btnSymmetricDifference_Click(object sender, EventArgs e)
{
HashSet<int> SymmetricDifference = new HashSet<int>();
foreach (int element in A)
SymmetricDifference.Add(element);
SymmetricDifference.SymmetricExceptWith(B);
lbxSymmetricDifference.Items.Clear();
foreach (int element in SymmetricDifference)
lbxSymmetricDifference.Items.Add(element);
}
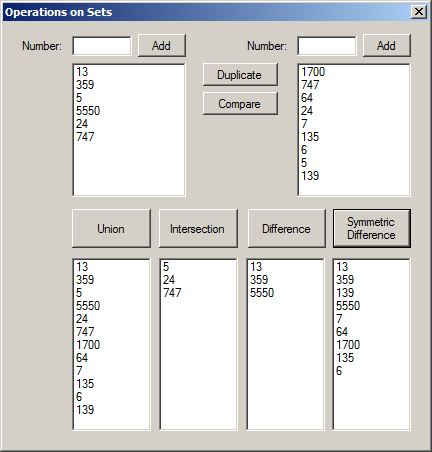
Deleting Items From a Set
Deleting an Item
The HashSet<> class implements the ICollection<> interface. As such, it inherits the Remove() method that allows you to delete an item from the list. Here is an example of calling it:
namespace Dictionaries
{
public partial class Exercise : Form
{
HashSet<string>? states;
public Exercise()
{
InitializeComponent();
}
private void PopulateSet()
{
lbxStates.Items.Clear();
foreach (string state in states!)
lbxStates.Items.Add(state);
}
private void Exercise_Load(object sender, EventArgs e)
{
states = new();
states.Add("Texas");
states.Add("Florida");
states.Add("Montana");
states.Add("Maryland");
states.Add("New York");
states.Add("California");
states.Add("North Carolina");
PopulateSet();
}
private void btnDelete_Click(object sender, EventArgs e)
{
states!.Remove("Montana");
PopulateSet();
}
}
}
Here is an example of running the program:
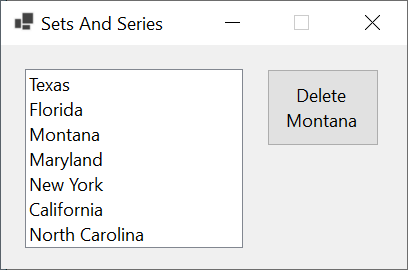
In some cases, you may want to delete an element based on a specific condition. To support this operation, the HashSet<> class provides a method named RemoveWhere. Its syntax is:
public int RemoveWhere(Predicate<T> match);
This method takes as argument a delegate that specifies what condition would be applied to any element that must be removed. Here is an example:
private void btnDelete_Click(object sender, EventArgs e)
{
states!.Remove(state => state == "Montana");
PopulateSet();
}
Clearing a Set
As an implementer of the ICollection interface, the HashSet<> class inherits the Clear() method that can be used remove all items from a set.
![]() Practical Learning: Clearing a Set
Practical Learning: Clearing a Set
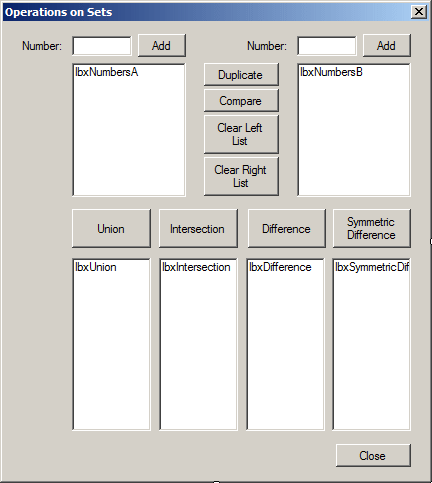
| Control | Text | Name | |
| Button | Clear Left List | btnClearLeftList | |
| Button | Clear Right List | lbxClearRightList | |
| Button | Close | btnClose | |
namespace SetsAndSeries
{
public partial class Algebra : Form
{
HashSet<int>? A;
HashSet<int>? B;
public Algebra()
{
InitializeComponent();
}
private void Algebra_Load(object sender, EventArgs e)
{
A = new HashSet<int>();
B = new HashSet<int>();
}
private void btnAddA_Click(object sender, EventArgs e)
{
int x;
try
{
x = int.Parse(txtNumberA.Text);
A!.Add(x);
}
catch (FormatException)
{
MessageBox.Show("The value you typed is not a valid number.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
lbxNumbersA.Items.Clear();
foreach (int element in A)
lbxNumbersA.Items.Add(element);
txtNumberA.Text = "";
txtNumberA.Focus();
}
private void btnDuplicate_Click(object sender, EventArgs e)
{
B = A;
foreach (int element in B)
lbxNumbersB.Items.Add(element);
}
private void btnCompare_Click(object sender, EventArgs e)
{
if (A!.SetEquals(B))
MessageBox.Show("A is equal to B",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is different from B",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSubsetOf(B))
MessageBox.Show("A is a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsSupersetOf(B))
MessageBox.Show("A is a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsProperSubsetOf(B))
MessageBox.Show("A is a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper sub-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.IsProperSupersetOf(B))
MessageBox.Show("A is a proper super-set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A is not a proper super set of B.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
if (A.Overlaps(B))
MessageBox.Show("A and B overlap.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
else
MessageBox.Show("A and B do not overlap.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
private void btnAddB_Click(object sender, EventArgs e)
{
int x;
try
{
x = int.Parse(txtNumberB.Text);
B!.Add(x);
}
catch (FormatException)
{
MessageBox.Show("The value you typed is not a valid number.",
"Algebra of Sets",
MessageBoxButtons.OK, MessageBoxIcon.Information);
}
lbxNumbersB.Items.Clear();
foreach (int element in B)
lbxNumbersB.Items.Add(element);
txtNumberB.Text = "";
txtNumberB.Focus();
}
private void btnUnion_Click(object sender, EventArgs e)
{
// Because objects in C# are used as references,
// we will need a brand new set that has the same
// elements as set A
HashSet<int> Union = new;
// Copy the elements of A into the new set
foreach (int element in A)
Union.Add(element);
// Unite the new set to B
Union.UnionWith(B);
lbxUnion.Items.Clear();
foreach (int element in Union)
lbxUnion.Items.Add(element);
}
private void btnIntersection_Click(object sender, EventArgs e)
{
var Intersection = new HashSet<int>();
foreach (int element in A)
Intersection.Add(element);
Intersection.IntersectWith(B);
lbxIntersection.Items.Clear();
foreach (int element in Intersection)
lbxIntersection.Items.Add(element);
}
private void btnDifference_Click(object sender, EventArgs e)
{
HashSet<int> Difference = new();
foreach (int element in A!)
Difference.Add(element);
Difference.ExceptWith(B!);
lbxDifference.Items.Clear();
foreach (int element in Difference)
lbxDifference.Items.Add(element);
}
private void btnSymmetricDifference_Click(object sender, EventArgs e)
{
var SymmetricDifference = new HashSet<int>();
foreach (int element in A!)
SymmetricDifference.Add(element);
SymmetricDifference.SymmetricExceptWith(B);
lbxSymmetricDifference.Items.Clear();
foreach (int element in SymmetricDifference)
lbxSymmetricDifference.Items.Add(element);
}
private void btnClearLeftList_Click(object sender, EventArgs e)
{
A!.Clear();
lbxNumbersA.Items.Clear();
txtNumberA.Focus();
}
private void btnClearRightList_Click(object sender, EventArgs e)
{
B!.Clear();
lbxNumbersB.Items.Clear();
txtNumberB.Focus();
}
private void btnClose_Click(object sender, EventArgs e)
{
Close();
}
}
}| Previous | Copyright © 2014-2023, FunctionX | Saturday 19 November 2022 | Next |