Home

Introduction to Date Values

Data Import/Export

Introduction

A date is a non-spatial value that uses a combination of numbers, symbols, and strings (or names). Both Microsoft Access and the Visual Basic language provide a great deal of support for date and time values.

Practical LearningPractical Learning: Introducing Date Values

  1. Start Microsoft Access
  2. In the list of files, click Exercise2 from Lesson 8
  3. On the Ribbon, click Create and click Form Design
  4. In the Controls section of the Ribbon, click the Button and click the form.
    If a wizard starts, click Cancel
  5. On the form, right-click the button and click Build Event...

The Date Data Type

To support dates and time values, the Visual Basic lanaguage includes a data type named Date.

Creating a Date Value

To create a date or a time value, declare a variable using the Date data type. Here is an example:

Private Sub Command0_Click()
    Dim DateHired As Date
End Sub

There are various format you can use to initialize a date or time variable. The numbers are represented with:

When initializing the variable, if you want to provide a constant value, you must include it between # and #. If you want to provide only two digits for the year, you can use one of the following formula:

If you will use all four digits for the year, you can use one of the following formula:

You can also use one of the following formats:

This time, enter the day value followed either by an empty space or -. Follow with the short name of the month in the mmm placeholder or the complete name of the month for the mmmm placeholder, followed by either an empty space or -. End the value with the year, using 2 or 4 digits.

As you may know already, in US English, you can start a date with the month. In this case, you can use one of the following formats:

As seen with the previous formats, mmm represents the short name of a month and mmmm represents the full name of a month. As mentioned already, the dd day can be expressed with 1 or 2 digits and the single digit can have a leading 0. After the day value, (you must) enter a comma followed by the year either with 2 or 4 digits.

A Serial Date

As an alternative to initiate the variable, the Visual Basic language provides a function named DateSerial. Its syntax is:

Public Function DateSerial(ByVal Year As Integer,
			   ByVal Month As Integer,
			   ByVal Day As Integer) As Date

Here is an example:

Private Sub Command0_Click()
    Dim DateHired As Date

    DateHired = DateSerial(2018, 8, 22)
End Sub

Converting a Value to Date

To let you convert a value to date or time, the Visual Basic language provides a function named CDate. Its syntax is:

Function CDate(Value As Variant) As Date

This function can take any type of value but the value must be convertible to a valid date. If the function succeeds in the conversion, it produces a Date value. If the conversion fails, it produces an error.

Of course, to convert a date value to string, you can call the CStr() function.

Practical Learning: Converting a Value to Date

  1. Type the following code: 
    Private Sub Command0_Click()
    Dim show
    Dim depart
    Dim d

    show = "05-30-2018"
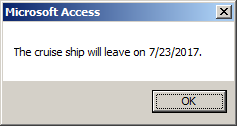
    depart = CDate("07/23/2017")
    d = CDate(show)
    
    MsgBox "The TV show will premiere on " & d & "."
    MsgBox "The cruise ship will leave on " & depart & "."
End Sub
  2. Return to Microsoft Access and switch the the form to Form View
  3. Click the button:

    Converting a Value to Date or Time

    Converting a Value to Date or Time

  4. Click OK on each message box
  5. Return to Microsoft Visual Basic
  6. As an alternative, you can call a function named DateValue. Its syntax is: 
    Public Function DateValue(StringDate As String) As Date
    For some examples, change the code as follows: 
    Private Sub Command0_Click()   
    Dim show
    Dim depart
    Dim d

    show = "05-30-2018"
    depart = DateValue("07/23/2017")
    d = DateValue(show)
    
    MsgBox "The TV show will premiere on " & d & "."
    MsgBox "The cruise ship will leave on " & depart & "."
End Sub
  7. Return to Microsoft Access and click the button
  8. Click OK on each message box
  9. Return to Microsoft Visual Basic

The Current System Date

To let you get the current date of the computer on which your database is used, the Visual Basic language provides a function named Date. Its syntax is:

Public Function Date() As Date

You can also consider that the function returns a string, in which case you can write it as Date$.

Practical Learning: Getting the Current System Date

  1. Change the code as follows: 
    Private Sub Command0_Click()
    MsgBox "Today is: " & Date
End Sub
  2. Return to Microsoft Access and click the button
  3. Click OK on the message box
  4. Return to Microsoft Visual Basic

Formatting the Display of Dates

Introduction

To assist you in controlling how a date value should display, the Visual Basic language provides a function named FormatDateTime. Its syntax is:

Public Function FormatDateTime(ByVal Expression As Date,
			       ByVal NamedFormat As VbDateTimeFormat) As String

The language also provides the Format() function. As a reminder, its syntax is:

Public Function Format(ByVal Expression As Variant, ByVal Style As String) As String

Remember that the first argument is the date that needs to be formatted. The second argument is a string that contains the formatting to apply. To create it, you use a combination of the month, day, and/or year characters we saw as date formats. Here is an example:

Private Sub cmdDateTime_Click()
    Dim DateHired As Date

    DateHired = #12/28/2006#
    MsgBox "Date Hired: " & Format(DateHired, "MMMM dd, yyyy")
End Sub

The Short Date Format

A short date format consists of presenting a date value with digits only. To display the short date format, pass the second argument of the FormatDateTime() function as vbShortDate.

Practical Learning: Using the Short Date Format

  1. Type the following code: 
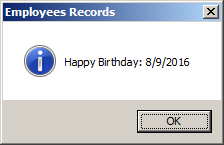
    Private Sub Command0_Click()
    Dim happy As Date

    happy = Date
    
    MsgBox "Happy Birthday: " & _
           FormatDateTime(happy, VbDateTimeFormat.vbShortDate), _
           vbOKOnly Or vbInformation, "Employees Records"
End Sub
  2. Return to Microsoft Access and click the button:

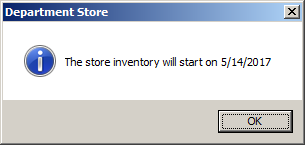
    The Short Date Format

  3. Click OK on the message box
  4. As an alternative, you can pass the second argument of the Format() function as Short Date (case-incensitive). For an example, return to Microsoft Visual Basic and change the code as follows: 
    Private Sub Command0_Click()
    Dim inventoryDate

    inventoryDate = #2017-05-14#
    
    MsgBox "The store inventory will start on " & _
	   Format(inventoryDate, "short date"), _
           vbOKOnly Or vbInformation, "Department Store"
End Sub
  5. Return to Microsoft Access and click the button:

    The Short Date Format

  6. Click OK on the message box and return to Microsoft Visual Basic

The Long Date Format

A long date format presents a date with the names of the day and of the month. To display the long date format, pass the second argument of the FormatDateTime() function as VbDateFormat.VbLongDate.

The Format() function provides more options to control how a date or one of its components (day, month, and/or year) appear.

Practical Learning: Using the Long Date Format

  1. Type the following code: 
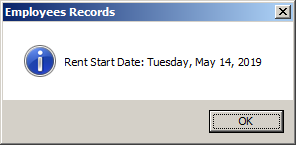
    Private Sub Command0_Click()
    Dim rentStart

    rentStart = #5/14/2019#
    
    MsgBox "Rent Start Date: " & _
	   FormatDateTime(rentStart, vbDateFormat.vbLongDate), _
           vbOKOnly Or vbInformation, "Employees Records"
End Sub
  2. Return to Microsoft Access and click the button:

    The Long Date Format

  3. Click OK on the message box and return to Microsoft Visual Basic
  4. As an alternative, you can pass the second argument of the Format() function as Long Date (case-insensitive). For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim inventoryDate

    inventoryDate = #2017-05-14#
    
    MsgBox "The store inventory will start on " & _
	   Format(inventoryDate, "long date"), _
           0, "Employees Records"
End Sub
  5. Return to Microsoft Access and click the button:

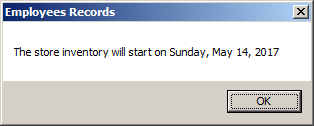
    Creating a Date Value

  6. Click OK on the message box and return to Microsoft Visual Basic

The Parts of a Date

The First Day of the Week

A week is a combination of 7 consecutive days. Each day can be recognized by an index from 1 to 7 (1, 2, 3, 4, 5, 6, 7). The day of each index is recognized by a name. In US English, the first day has an index of 1 is named Sunday while the last day with an index of 7 is named Monday. The days of a week have long and short names. These are:

US English Day Index Full Name Short Name
1 Sunday Sun
2 Monday Mon
3 Tuesday Tue
4 Wednesday Wed
5 Thursday Thu
6 Friday Fri
7 Saturday Sat

When performing operations on date (and time) values, you must indicate on what day of the week to start counting the days. By default, the Visual Basic language considers that a week starts on a Sunday. This means that the date system of the Visual Basic language considers Sunday as the first day of the week. Most or all functions allow you to specify a different day. To support this, the Visual Basic language provides an enumeration named FirstDayOfWeek. Its members are:

FirstDayOfWeek Member Value Weekday
vbUseSystem 0 The system will manage it
vbSunday 1 Sunday
vbMonday 2 Monday
vbTuesday 3 Tuesday
vbWednesday 4 Wednesday
vbThursday 5 Thursday
vbFriday 6 Friday
vbSaturday 7 Saturday

The Part Name of a Date Value

The Visual Basic language provides various options to get the day, the month, or the year of an existing date value. One of the functions used is named DatePart. Its syntax is:

Public Function DatePart(ByVal Interval As DateInterval,
			 ByVal DateValue As Date,
			 ByVal Optional FirstDayOfWeekValue As FirstDayOfWeek,
			 ByVal Optional FirstWeekOfYearValue As FirstWeekOfYear) As Integer

The first argument, required, specifies the type of value to get. The second argument, also required, is the date from which to get the value.

The Day of a Date

To get the day in the month of a date value, you can call a function named Day. Its syntax is:

Public Function Day(ByVal DateValue As Date) As Integer

This function takes a date as argument and produces its day.

Practical Learning: Getting the Day of a Date Value

  1. Type the following code: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/12/1975#
    d = Day(dob)

    MsgBox "Day: " & d, 0 Or 64, "Employees Records"
End Sub
  2. Return to Microsoft Access and click the button
  3. Click OK on the message box and return to Microsoft Visual Basic
  4. As an alternative, you can call the DatePart() function and pass the second argument as "d". For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/12/1975#
    d = DatePart("d", dob)

    MsgBox "Day: " & d, 0 Or 64, "Employees Records"
End Sub
  5. Return to Microsoft Access and click the button
  6. Click OK on the message box and return to Microsoft Visual Basic
  7. One more alternative is to call the Format() function and pass the second argument as: "d": If the number of the day is less than 10, it will be produced with that digit. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "d")

    MsgBox "Day: " & d, 64, "Employees Records"
End Sub
  8. Return to Microsoft Access and click the button
  9. Click OK on the message box and return to Microsoft Visual Basic
  10. When calling the Format() function, if you pass the second argument as "dd", if the number of the day is less than 10, it will be produced with a leading 0. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "dd")

    MsgBox "Day: " & d, 0 Or 48, "Employees Records"
End Sub
  11. Return to Microsoft Access and click the button
  12. Click OK on the message box and return to Microsoft Visual Basic

The Month Name of a Date

In US English, the names of months are January, February, March, April, May, June, July, August, September, October, November, and December. These are also referred to as the long names of months. A month is recognized by an index in a range from 1 to 12. The long and short names of months, including their indexes, can be resumed as follows:

Month Index Full Name Short Name
1 January Jan
2 February Feb
3 March Mar
4 April Apr
5 May May
6 June Jun
7 July Jul
8 August Aug
9 September Sep
10 October Oct
11 November Nov
12 December Dec

In a formatting scenario, the long name of a month is represented as MMMM. As a result, using these names, you can initialize a Date variable using one of the following formats:

A short name of a month is a simplified version of a long name. It uses three letters for the month. Except for the month of May, the short names of months are Jan, Feb, Mar, Apr, Jun, Jul, Aug, Sep, Oct, Nov, and Dec. The short are represented in a format as MMM. As a result, you can initialize a Date variable using one of the following formats:

To let you get the name of the month of a date, the Visual Basic language provides a function named MonthName. Its syntax is:

Public Function MonthName(ByVal month As Integer, ByVal abbreviate As Boolean) As String

The first argument is required and it is just the numeric position of a month within a year.

If you provide only the first argument, the function produces the long name of the month. If you want a short name for the month, pass the second argument as True.

Practical Learning: Getting the Month of a Date Value

  1. Type the following code: 
    Private Sub Command0_Click()
    MsgBox "Month: " & MonthName(8), 48, "Exercise"
End Sub
  2. Return to Microsoft Access and click the button:

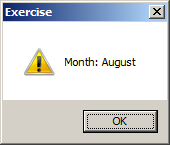
    The Month of a Date

  3. Click OK on the message box and return to Microsoft Visual Basic

The Numeric Month of a Date

To get the numeric position of a month in a date, you can call a function named Month. Its syntax is:

Public Function Month(ByVal DateValue As Date) As Integer

Practical Learning: Getting the Numeric Month of a Date Value

  1. Type the following code: 
    Private Sub Command0_Click()
    Dim vote
    
    vote = #2/20/2016#
    
    MsgBox Month(vote), 0 Or 64, "Citizens Issues"
End Sub
  2. Return to Microsoft Access and click the button
  3. As you can see, the Month() function returns an integer that is the position or index of the month. You can pass that return value to the MonthName() function.
    Click OK on the message box and return to Microsoft Visual Basic
  4. Change the code as follows: 
    Private Sub Command0_Click()
    Dim vote
    
    vote = #2/20/2016#
    
    MsgBox MonthName(Month(vote)), 64, "Citizens Issues"
End Sub
  5. Return to Microsoft Access and click the button:

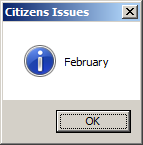
    The Numeric Month of a Date

  6. Click OK on the message box and return to Microsoft Visual Basic
  7. As an alternative, you can call the DatePart() function and pass the first argument as "m" or "M". For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim start
    
    start = #4/11/2008#
    
    MsgBox DatePart("m", start), _
           vbOKOnly Or vbInformation, _
           "Sport Season"
End Sub
  8. Return to Microsoft Access and click the button
  9. Click OK on the message box and return to Microsoft Visual Basic
  10. As another alternative, you can call the Format function and pass the second argument as "m". In this case, if the numeric position of the month is less than 10, it will be produced with that digit. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "M")

    MsgBox "Month: " & d, _
           vbOKOnly Or vbInformation, "Employees Records"
End Sub
  11. Return to Microsoft Access and click the button
  12. Click OK on the message box and return to Microsoft Visual Basic
  13. You can pass the argument as "mm". In this case, if the numeric position of the month is less than 10, the function will produce the number with a leading 0. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "MM")

    MsgBox "Month: " & d, _
           vbOKOnly Or vbInformation, _
           "Employees Records"
End Sub
  14. Return to Microsoft Access and click the button
  15. Click OK on the message box and return to Microsoft Visual Basic
  16. You can pass the argument as "mmm". In this case, the function will return the short name of the month. For an example example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "MMM")

    MsgBox "Month: " & d, _
           vbOKOnly Or vbInformation, "Employees Records"
End Sub
  17. Return to Microsoft Access and click the button
  18. Click OK on the message box and return to Microsoft Visual Basic
  19. You can pass the argument as "mmmm". In this case, the function will return the long name of the month. Here is an example: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "MMMM")

    MsgBox "Month: " & d, _
           vbOKOnly Or vbInformation, "Employees Records"
End Sub
  20. Return to Microsoft Access and click the button
  21. Click OK on the message box and return to Microsoft Visual Basic
  22. One of the advantages of the Format() function is that it already has that functionality built-in. This means that you can combine letters and symbols in the second argument of that function. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Format(dob, "mmmm dd")

    MsgBox "Birthday: " & d, _
           vbOKOnly Or vbInformation, _
           "Employees Records"
End Sub
  23. Return to Microsoft Access and click the button:

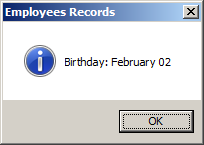
    Formatting a Date

  24. Click OK on the message box and return to Microsoft Visual Basic

The Year of a Date

To let you get the year of a date, the Visual Basic language provides a function named Year. Its syntax is:

Public Function Year(DateValue As Date) As Integer

Practical Learning: Getting the Year of a Date Value

  1. Type the following code: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim d

    dob = #2/2/1975#
    d = Year(dob)
    MsgBox "Year: " & d, _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "Student Registration"

End Sub
  2. Return to Microsoft Access and click the button
  3. Click OK on the message box and return to Microsoft Visual Basic
  4. Another way to get the year value is to call the DatePart() function. You can pass the first argument as "y". In this case, the function will produce the number of days since January 1st of the year in the date. For an example, type the following code: 
    Private Sub Command0_Click()
    Dim d
    Dim dob As Date
    Dim number As Long
    
    dob = DateSerial(Year(Date) - CInt(Int((40 * Rnd()) + 1)), _
                                  CInt(Int((12 * Rnd()) + 1)), _
                                  CInt(Int((28 * Rnd()) + 1)))
    
    d = DatePart("y", dob)

    MsgBox "The student was born on day " & d & " of " & CStr(Year(dob)), _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "Student Registration"
End Sub
  5. Return to Microsoft Access and click the button:

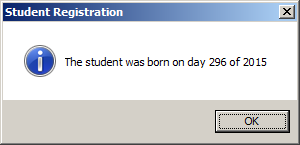
    The Year of a Date

  6. Click OK on the message box and return to Microsoft Visual Basic
  7. You can pass the interval as "yyyy". In this case, the function will produce the four-digit year of the date. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim d
    Dim dob As Date
    Dim number As Long
    
    dob = DateSerial(Year(Date) - CInt(Int((40 * Rnd()) + 1)), _
                                  CInt(Int((12 * Rnd()) + 1)), _
                                  CInt(Int((28 * Rnd()) + 1)))

    d = DatePart("yyyy", dob)

    MsgBox "The student was born in " & CStr(d), _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "Student Registration"
End Sub
  8. Return to Microsoft Access and click the button:

    The Year of a Date

  9. Click OK on the message box and return to Microsoft Visual Basic
  10. One more alternative is to call the Format() function and pass the second argument as "y". In this case, the function will produce the number of days since January 1st of the year in the date. To apply an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim d
    Dim dob As Date
    Dim number As Long
    
    dob = DateSerial(Year(Date) - CInt(Int((40 * Rnd()) + 1)), _
                                  CInt(Int((12 * Rnd()) + 1)), _
                                  CInt(Int((28 * Rnd()) + 1)))
    d = Format(dob, "y")
    MsgBox "Date of Birth: " & CStr(dob) & vbCrLf & _
           "The person was born on day " & d & " of " & CStr(Year(dob)), _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "National Census"
End Sub
  11. Return to Microsoft Access and click the button:

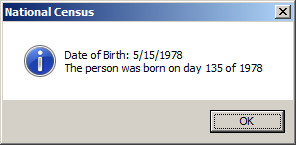
    The Year of a Date

  12. Click OK on the message box and return to Microsoft Visual Basic
  13. You can pass the argument as "yy". In this case, the function will produce the right two digits of the year of the date. For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim d
    Dim dob As Date
    Dim number As Long
    
    dob = DateSerial(Year(Date) - CInt(Int((40 * Rnd()) + 1)), _
                                  CInt(Int((12 * Rnd()) + 1)), _
                                  CInt(Int((28 * Rnd()) + 1)))
    d = Format(dob, "yy")
    MsgBox "Date of Birth: " & CStr(dob) & vbCrLf & _
           "The last two digits of the year a " & d & ".", _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "National Census"
End Sub
  14. Return to Microsoft Access and click the button:

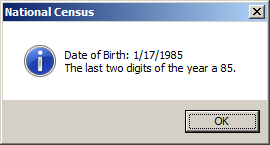
    The Year of a Date

  15. Click OK on the message box and return to Microsoft Visual Basic
  16. You can pass the argument as "yyy". In this case, the function will produce a combination of the above two formats: A string that contains the right two digits of the year of the date followed by the number of days of that date.  For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim d
    Dim dob As Date
    Dim number As Long
    
    dob = DateSerial(Year(Date) - CInt(Int((40 * Rnd()) + 1)), _
                                  CInt(Int((12 * Rnd()) + 1)), _
                                  CInt(Int((28 * Rnd()) + 1)))
    d = Format(dob, "yyy")
    MsgBox "Date of Birth: " & CStr(dob) & vbCrLf & _
           "The last two digits of the year a " & d & ".", _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "National Census"
End Sub
  17. Return to Microsoft Access and click the button:

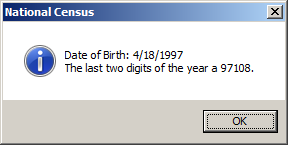
    The Year of a Date

  18. Click OK on the message box and return to Microsoft Visual Basic
  19. You can pass the argument as "yyyy". In this case, the function will produce the year of the date.  For an example, change the code as follows: 
    Private Sub Command0_Click()
    Dim d
    Dim dob As Date
    Dim number As Long
    
    dob = DateSerial(Year(Date) - CInt(Int((40 * Rnd()) + 1)), _
                                  CInt(Int((12 * Rnd()) + 1)), _
                                  CInt(Int((28 * Rnd()) + 1)))
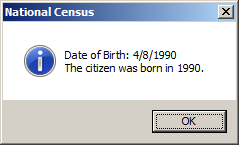
    d = Format(dob, "yyyy")
    MsgBox "Date of Birth: " & CStr(dob) & vbCrLf & _
           "The citizen was born in " & d & ".", _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "National Census"
End Sub
  20. Return to Microsoft Access and click the button:

    The Year of a Date

  21. Click OK on the message box and return to Microsoft Visual Basic

The Week Day

To let you get the index of a day of the week in which a date occurs, the Visual Basic language provides the Weekday() function. Its syntax is:

Public Function Weekday(ByVal DateValue As Date,
			ByVal DayOfWeek As FirstDayOfWeek) As Integer

The first argument is required and is a date that will be considered.

To let you get the name of a day in a week, the Visual Basic language provides a function named WeekdayName. Its syntax is:

Public Function WeekdayName(ByVal Weekday As Integer,
		            ByVal Abbreviate As Boolean,
			    ByVal FirstDayOfWeekValue As FirstDayOfWeek) As String

The first argument of the WeekdayName() function is the only one required. It is the numeric index of a day in a week. The third argument follows the same logic as the second argument of the Weekday() function.

Practical Learning: Getting the Week Day of a Date Value

  1. Change the code as follows: 
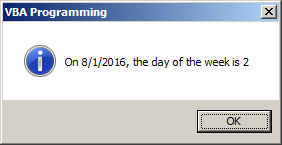
    Private Sub Command0_Click()
    Dim dteStart As Date

    dteStart = DateSerial(2016, 8, 1)

    MsgBox "On " & dteStart & ", the day of the week is " & Weekday(dteStart), _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "VBA Programming"
End Sub
  2. Return to Microsoft Access and click the button:

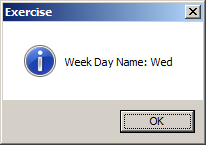
    The Week Day

  3. Click OK on the message box and return to Microsoft Visual Basic
  4. For an example of calling the Weekday() function, type the following code: 
    Private Sub Command0_Click()
    MsgBox "Week Day Name: " & WeekdayName(1), 64, "Exercise"
End Sub
  5. Return to Microsoft Access and click the button:

    The Week Day

    As you can see, by default, this function produces the full name of a week day. Click OK on the message box and return to Microsoft Visual Basic

  6. If you want a short name, pass the second argument as True. For an example, change the code as follows: 
    Private Sub Command0_Click()
    MsgBox "Week Day Name: " & WeekdayName(4, True), 64, "Exercise"
End Sub
  7. Return to Microsoft Access and click the button:

    The Week Day

  8. Click OK on the message box and return to Microsoft Visual Basic

Operations on Date Values

Adding a Number to a Date Value

Date addition consists of adding a number of days, months, or years, to a date value. To support this operation, the Visual Basic language provides a function named DateAdd. Its syntax is:

Public Function DateAdd(ByVal Interval As String,
			ByVal Number As Integer,
		        ByVal DateValue As Date) As Date

The first argument specifies the type of value that will be added. It can be one of the following values:

Date Interval String
d The number of days to add to the date value
y The number of days of a year to add to the date value
w The number of days to add to the date value
ww The number of weeks to add to the date value
m A number of months to add to the date value
yyyy A number of years to add to the date value
q A number of quarters of a year to add to the date value

Practical Learning: Getting the Week Day of a Date Value

  1. For an example that adds two days to a date value, type the following code: 
    Private Sub Command0_Click()
    Dim dob As Date
    Dim today As Date
    Dim passed As Date

    dob = #8/10/1995#
    today = Date
    passed = DateAdd("y", 2, dob)
    
    MsgBox "A New Date: " & passed, 64, "Exercise"
End Sub
  2. Return to Microsoft Access and click the button:

    Date Addition

  3. Click OK on the message box and return to Microsoft Visual Basic

The Difference Between Two Date Values

To let you find the difference between two dates, the Visual Basic language provides a function named DateDiff. Its syntax is:

Public Function DateDiff(ByVal Interval As DateInterval,
			 ByVal Date1 As Date,
			 ByVal Date2 As Date,
			 ByVal DayOfWeek As FirstDayOfWeek,
			 ByVal WeekOfYear As FirstWeekOfYear) As Long

The first argument specifies the type of value the function must produce. This argument uses the same value as those of the DateAdd() function. The second argument is the starting date. The third argument is the end date. Those three arguments are the only ones required.

Practical Learning: Getting the Week Day of a Date Value

  1. Type the code as follows: 
    Private Sub Command0_Click()
    Dim days
    Dim years
    Dim dteEnd
    Dim months
    Dim dteStart

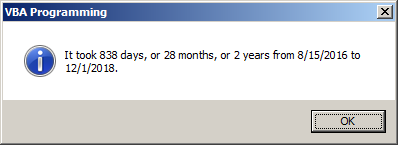
    dteStart = DateSerial(2016, 8, 15)
    dteEnd = DateSerial(2018, 12, 1)

    days = DateDiff("d", dteStart, dteEnd)
    months = DateDiff("m", dteStart, dteEnd)
    years = DateDiff("yyyy", dteStart, dteEnd)
    
    MsgBox "It took " & days & " days, or " & months & _
           " months, or " & years & " years from " & dteStart & " to " & dteEnd & ".", _
           VbMsgBoxStyle.vbOKOnly Or VbMsgBoxStyle.vbInformation, _
           "VBA Programming"
End Sub
  2. Return to Microsoft Access and click the button:

    The Difference Between Two Date Values

  3. Click OK on the message box
  4. Close the form
  5. When asked whether you want to save, click No
Previous Copyright © 2008-2022, FunctionX, Inc. Next